猫　算

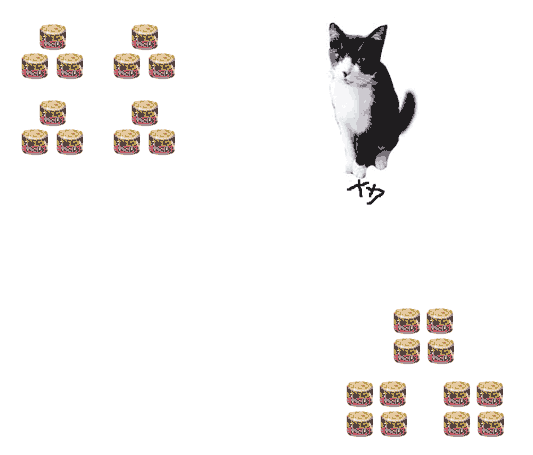
どちらを選ぶべきか。

すくなくとも、
●●●＜●●●●
ということくらい、
彼ならわかりそうな気がするが・・・
いややっぱり「数える」ということは、
そう簡単ではないのだろうか。

ましてや、
●●●
●●●
●●●
●●●
＝
●●●●
●●●●
●●●●
と「かけ算」しているなんてことは、
絶対ありえないのだろうか。

われわれ人なら、
缶の数はどちらも同じだとすぐわかる。
それは、
●＝１、●●＝２、●●●＝３、●●●●＝４・・・を
まず理解し、さらに、
●●●+●●●+●●●+●●●＝
●●●●+●●●●+●●●●
すなわち、3×4＝12、4×3＝12を
理解しているからだろう。
そのうち３個や４個の物が並んだ形を覚え、
さらには12個の物が並んだ形も覚えてしまうだろう。

しかし、われわれも大昔の大昔は、
満腹の度合いで比べるしかなかったのだろうか。
でもあるとき誰かが、
「数える」ことに気づき、
さらにあるとき誰かが
「かけ算」をあみだす。
そしてわれわれは九九を覚えさせられる。

もういっかい彼の頭の中に戻ろう。
彼の頭の働きと、われわれの頭の働きとの
決定的な違いの一つは「言語」の有無だろう。

だがしかし、
●●●＜●●●●
とか、
●●●×●●●●＝
●●●●×●●●
ということが「わかる」ために、
言語は絶対に不可欠なのだろうか。
どうもそうではないような気がしてくる。

あるいは
Ａ＞ＢかつＢ＞ＣならＡ＞Ｃ
といったことも、
もともと言語とは無関係の法則なのではなかろうか。
どうなんだろうか。

野矢茂樹が『はじめて考えるときのように』で、
「足し算に答えるのに考える必要なんかない」
「論理は考えないためにある」
と述べていたことを思い出す。

一方、信原幸弘という人が、
『考える脳・考えない脳』（講談社現代新書）で、
暗算は脳の中ではなく外で操作されている、
といった趣旨のことを述べていたことも思い出す。
これは、
たとえば4×3を計算するとき、
あるいは24×7を計算するとき、
ニューロンにおいて、
4単位や3単位、あるいは24単位や7単位の
目盛りに対応するような反応が起こっているわけではない、
ということだろう。

いや、ぐだぐだ述べたけれど、
３缶×４と、４缶×３が、同じであるということに
彼はなんらか独自のやり方で気付けるのではないか。
しかもそのやり方は、
根っこのところでは、われわれのやり方と同一なのではないか。
そうした疑問が頭を離れないのです。
どう思いますか。